blackboard

waynehu

Professor, Department of Astronomy and Astrophysics
University of Chicago

Group Contact CV SnapShots
CMB Introduction '96   Intermediate '01   Polarization Intro '01   Cosmic Symphony '04   Polarization Primer '97   Review '02   Power Animations   Lensing   Power Prehistory   Legacy Material '96   PhD Thesis '95 Baryon Acoustic Oscillations Cosmic Shear Clusters
Transfer Function
Intro to Cosmology [243] Cosmology I [legacy 321] Cosmology II [321] Current Topics [282] Galaxies and Universe [242] Radiative Processes [305] Research Preparation [307] GR Perturbation Theory [408] CMB [448] Cosmic Acceleration [449]


Parameter Sensitivity

The phenomenology of the acoustic peaks in the temperature and polarization is essentially described by 4 observables and the initial conditions [Hu et al, 1997]. These are the angular extents of the sound horizon $\ell_{\rm a}\equiv \pi D_*/s_*$, the particle horizon at matter radiation equality $\ell_{\rm eq} \equiv k_{\rm eq}D_*$ and the damping scale $\ell_{\rm d} \equiv k_{\rm d}D_*$ as well as the value of the baryon-photon momentum density ratio $R_*$. $\ell_{\rm a}$ sets the spacing between of the peaks; $\ell_{\rm eq}$ and $\ell_{\rm d}$ compete to determine their amplitude through radiation driving and diffusion damping. $R_*$ sets the baryon loading and, along with the potential well depths set by $\ell_{\rm eq}$, fixes the modulation of the even and odd peak heights. The initial conditions set the phase, or equivalently the location of the first peak in units of $\ell_{\rm a}$, and an overall tilt $n$ in the power spectrum.

\begin{plate} % latex2html id marker 582 %%3 \centerline{\epsfxsize=6in\epsffile... ...a_b h^2=0.02$, $\Omega_m h^2=0.147$, $n=1$, $z_{\rm ri}=0$, $E_i=0$.}\end{plate}

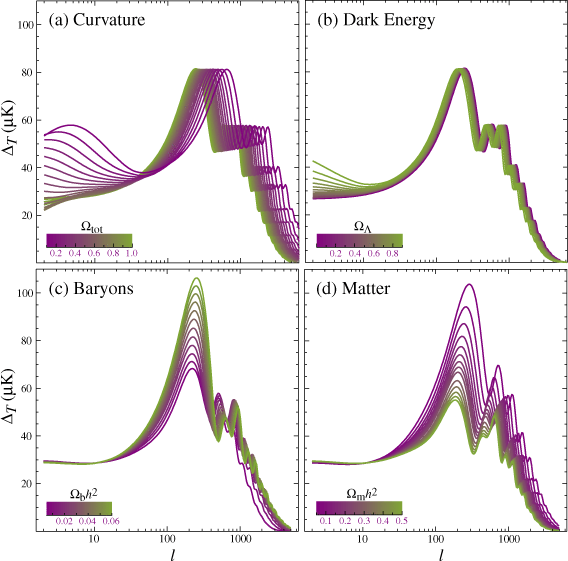
In the model of Plate 1, these numbers are $\ell_{\rm a}= 301$ ( $\ell_1=0.73\ell_{\rm a}$), $\ell_{\rm eq}= 149$, $\ell_{\rm d}=1332$, $R_*=0.57$ and $n=1$ and in this family of models the parameter sensitivity is approximately [Hu et al, 2001]

$\displaystyle {\Delta \ell_{\rm a}\over \ell_{\rm a}}$ $\textstyle \approx$ $\displaystyle -0.24 {\Delta \Omega_m h^2\over \Omega_m h^2} +0.07 {\Delta \Omeg... ...over \Omega_{\Lambda}} -1.1 {\Delta \Omega_{\rm tot}\over \Omega_{\rm tot}} \,,$  
$\displaystyle {\Delta \ell_{\rm eq} \over \ell_{\rm eq}}$ $\textstyle \approx$ $\displaystyle 0.5 {\Delta \Omega_m h^2\over \Omega_m h^2} -0.17 {\Delta \Omega_... ...over \Omega_{\Lambda}} -1.1 {\Delta \Omega_{\rm tot}\over \Omega_{\rm tot}} \,,$ (24)
$\displaystyle {\Delta \ell_{\rm d}\over \ell_{\rm d}}$ $\textstyle \approx$ $\displaystyle -0.21 {\Delta \Omega_m h^2\over \Omega_m h^2} +0.20 {\Delta \Omeg... ...ver \Omega_{\Lambda}} -1.1 {\Delta \Omega_{\rm tot} \over \Omega_{\rm tot}} \,,$  

and $\Delta R_*/R_* \approx 1.0 \Delta \Omega_b h^2/ \Omega_b h^2$. Current observations indicate that $\ell_{\rm a}= 304\pm 4$, $\ell_{\rm eq}=168 \pm 15$, $\ell_{\rm d}=1392 \pm 18$, $R_* = 0.60 \pm 0.06$, and $n = 0.96 \pm 0.04$ ([Knox et al, 2001]; see also [Wang et al, 2001,Pryke et al, 2001,de Bernardis et al, 2001]), if gravitational waves contributions are subdominant and the reionization redshift is low as assumed in the working cosmological model (see §2.1).

The acoustic peaks therefore contain three rulers for the angular diameter distance test for curvature, i.e. deviations from $\Omega _{\rm tot}=1$. However contrary to popular belief, any one of these alone is not a standard ruler whose absolute scale is known even in the working cosmological model. This is reflected in the sensitivity of these scales to other cosmological parameters. For example, the dependence of $\ell_{\rm a}$ on $\Omega _m h^2$ and hence the Hubble constant is quite strong. But in combination with a measurement of the matter-radiation ratio from $\ell_{\rm eq}$, this degeneracy is broken.

The weaker degeneracy of $\ell_{\rm a}$ on the baryons can likewise be broken from a measurement of the baryon-photon ratio $R_*$. The damping scale $\ell_{\rm d}$ provides an additional consistency check on the implicit assumptions in the working model, e.g. recombination and the energy contents of the Universe during this epoch. What makes the peaks so valuable for this test is that the rulers are standardizeable and contain a built-in consistency check.

There remains a weak but perfect degeneracy between $\Omega _{\rm tot}$ and $\Omega _\Lambda $ because they both appear only in $D_*$. This is called the angular diameter distance degeneracy in the literature and can readily be generalized to dark energy components beyond the cosmological constant assumed here. Since the effect of $\Omega _\Lambda $ is intrinsically so small, it only creates a correspondingly small ambiguity in $\Omega _{\rm tot}$ for reasonable values of $\Omega _\Lambda $. The down side is that dark energy can never be isolated through the peaks alone since it only takes a small amount of curvature to mimic its effects. The evidence for dark energy through the CMB comes about by allowing for external information. The most important is the nearly overwhelming direct evidence for $\Omega_m < 1$ from local structures in the Universe. The second is the measurements of a relatively high Hubble constant $h\approx 0.7$; combined with a relatively low $\Omega _m h^2$ that is preferred in the CMB data, it implies $\Omega_m < 1$ but at low significance currently.

The upshot is that precise measurements of the acoustic peaks yield precise determinations of four fundamental parameters of the working cosmological model: $\Omega _b h^2$, $\Omega _m h^2$, $D_*$, and $n$. More generally, the first three can be replaced by $\ell_{\rm a}$, $\ell_{\rm eq}$, $\ell_{\rm d}$ and $R_*$ to extend these results to models where the underlying assumptions of the working model are violated.

next up previous
Next: BEYOND THE PEAKS Up: ACOUSTIC PEAKS Previous: Integral Approach
Wayne Hu 2001-10-15