-bands
to increase the signal-to-noise (see Fig. 14 and
Table 2).
The main reason why polarization is so useful to the reconstruction process is that (cosmologically) it can only be generated by Thomson scattering. The polarization spectrum of the CMB is thus a direct snapshot of conditions on the last scattering surface. Contrast this with temperature fluctuations which can be generated by changes in the metric fluctuations between last scattering and the present, such as those created by gravitational potential evolution. This is the reason why the mere detection of large-angle anisotropies by COBE did not rule out wide classes of models such as cosmological defects. To use the temperature anisotropies for the reconstruction problem, one must isolate features in the spectrum which can be associated with last scattering, or more generally, the universe at a known redshift.
Furthermore, the polarization spectrum has potential advantages even
for extracting information from
features that are also present in the temperature
spectrum, e.g. the acoustic peaks. The polarization spectrum is
generated by local quadrupole anisotropies alone whereas the temperature
spectrum has comparable contributions from the local monopole and dipole
as well as possible contributions between last scattering and the present.
This property enhances the prominence of features (see Fig. 14)
as does the fact that the scalar polarization has a relatively sharp
projection due to the geometry (see §3.2).
Unfortunately, these considerations are mitigated by the fact that the
polarization amplitude is so much weaker than the temperature.
With present day detectors, one needs to measure it in broad -bands
to increase the signal-to-noise (see Fig. 14 and
Table 2).
Fig. 14: Temperature, polarization, and temperature-polarization cross correlation predictions and sensitivity of MAP for a fiducial model with &Omega0=1, &Omegab=0.1, and h=0.5 cold dark matter model. The raw MAP satellite sensitivity (1&sigma errors on the recovered power spectrum binned in l is approximated by wT-1/2= 0.11μK for the temperature and wT -1/2= 0.15μK for the polarization and a FWHM beam of 0.25deg. Note that errors between spectra are correlated. While the reionized model (purple &tau=0.1) is impossible to distinguish from the fiducial model from temperature anisotropies alone, its effect on polarization is clearly visible at low l. Dashed lines for temperature-polarization correlation represent anticorrelation.
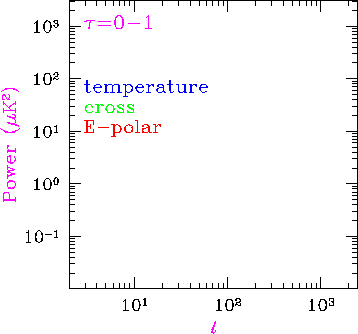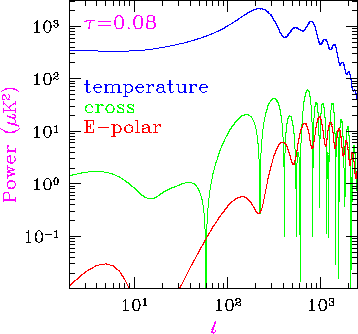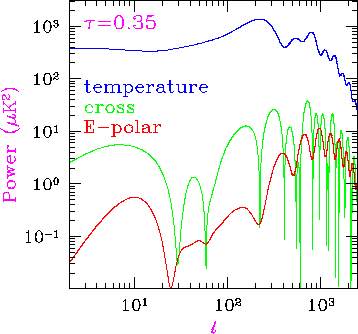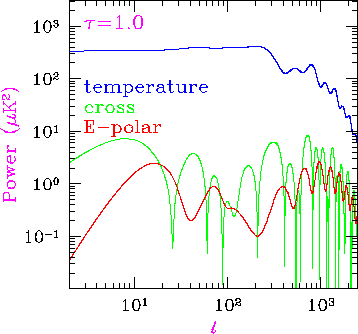
Animation: variations in the spectra as &tau is stepped from 0-1.
Next: Reionization