The most commonly considered and familiar types of perturbations are scalar modes. These modes represent perturbations in the (energy) density of the cosmological fluid(s) at last scattering and are the only fluctuations which can form structure though gravitational instability.
Consider a single large-scale Fourier component of the fluctuation, i.e. for the photons, a single plane wave in the temperature perturbation. Over time, the temperature and gravitational potential gradients cause a bulk flow, or dipole anisotropy, of the photons. Both effects can be described by introducing an ``effective'' temperature
![]()
where ![]() is the gravitational
potential. Gradients in the effective temperature always
create flows from hot to cold effective temperature. Formally,
both pressure and gravity act as sources of the momentum density
of the fluid in a combination that is exactly the effective temperature
for a relativistic fluid.
is the gravitational
potential. Gradients in the effective temperature always
create flows from hot to cold effective temperature. Formally,
both pressure and gravity act as sources of the momentum density
of the fluid in a combination that is exactly the effective temperature
for a relativistic fluid.
To avoid confusion, let us explicitly consider the case of adiabatic fluctuations, where initial perturbations to the density imply potential fluctuations that dominate at large scales. Here gravity overwhelms pressure in overdense regions causing matter to flow towards density peaks initially. Nonetheless, overdense regions are effectively cold initially because photons must climb out of the potential wells they create and hence lose energy in the process. Though flows are established from cold to hot temperature regions on large scales, they still go from hot to cold effective temperature regions. This property is true more generally of our adiabatic assumption: we hereafter refer only to effective temperatures to keep the argument general.
Let us consider the quadrupole component of the temperature pattern
seen by an observer located in a trough of a plane wave.
The azimuthal symmetry in the problem requires that
![]() and hence the flow is irrotational
and hence the flow is irrotational
![]() .
Because hotter photons from the crests flow into the trough from the
.
Because hotter photons from the crests flow into the trough from the
![]() directions
while cold photons surround the observer in the plane,
the quadrupole pattern seen in a
trough has an m=0,
directions
while cold photons surround the observer in the plane,
the quadrupole pattern seen in a
trough has an m=0,
![]()
structure
with angle ![]() (see Fig. 2).
The opposite effect occurs at the crests, reversing the sign of the
quadrupole but preserving the m=0 nature in its local angular dependence.
The full effect is thus described by a local quadrupole modulated by a plane
wave in space,
(see Fig. 2).
The opposite effect occurs at the crests, reversing the sign of the
quadrupole but preserving the m=0 nature in its local angular dependence.
The full effect is thus described by a local quadrupole modulated by a plane
wave in space, ![]() ,
where the sign denotes the fact that photons flowing into cold regions are
hot. This infall picture must be modified slightly on scales smaller than
the sound horizon where pressure plays a role (see §3.3.2),
however the essential property that the flows are parallel to
,
where the sign denotes the fact that photons flowing into cold regions are
hot. This infall picture must be modified slightly on scales smaller than
the sound horizon where pressure plays a role (see §3.3.2),
however the essential property that the flows are parallel to ![]() and
thus generate an m=0 quadrupole remains true.
and
thus generate an m=0 quadrupole remains true.
Fig. 2: The scalar quadrupole moment (l=2, m=0). Flows from hot (blue) regions into cold (red), produce the azimuthally symmetric pattern Y20.
The sense of the quadrupole moment determines the polarization pattern through
Thomson scattering.
Recall that polarized scattering peaks when the temperature varies in the
direction orthogonal to ![]() .
Consider then the tangent plane
.
Consider then the tangent plane ![]() with
normal
with
normal ![]() . This may be visualized in an angular ``lobe'' diagram
such as Fig. 2 as a plane which passes through the
``origin'' of the quadrupole pattern perpendicular to the line of sight.
The polarization is maximal when the hot and cold lobes of the quadrupole
are in this tangent plane, and is aligned with the component of the colder
lobe which lies in the plane.
As
. This may be visualized in an angular ``lobe'' diagram
such as Fig. 2 as a plane which passes through the
``origin'' of the quadrupole pattern perpendicular to the line of sight.
The polarization is maximal when the hot and cold lobes of the quadrupole
are in this tangent plane, and is aligned with the component of the colder
lobe which lies in the plane.
As ![]() varies from 0 to
varies from 0 to ![]() (pole to equator) the temperature
differences in this plane increase from zero (see Fig. 3a).
The local polarization at the crest of the temperature perturbation is thus
purely in the N-S direction tapering off in amplitude toward the poles
(see Fig. 3b).
This pattern represents a pure Q-field on the sky whose amplitude varies
in angle as an
(pole to equator) the temperature
differences in this plane increase from zero (see Fig. 3a).
The local polarization at the crest of the temperature perturbation is thus
purely in the N-S direction tapering off in amplitude toward the poles
(see Fig. 3b).
This pattern represents a pure Q-field on the sky whose amplitude varies
in angle as an ![]() , m=0 tensor or spin-2 spherical harmonic
, m=0 tensor or spin-2 spherical harmonic
![]()
In different regions of space, the plane wave modulation of the quadrupole can change the sign of the polarization, but not its sense.
Fig. 3: The transformation of quadrupole anisotropies into linear polarization. (a) The orientation of the quadrupole moment with respect to the scatterig direction n determines the sense and magnitude of the polarization. It is aligned with the cold (red, long) lobe in the e&thetaxe&phi tangent plane. (b) In spherical coordinates where n.k = cos θ, the polarization points north-south (Q) with magnitude varying as sin2θ for scalar fluctuations.
This pattern (Fig. 4, yellow lines) is of course not the
only logical possibility for an ![]() , m=0 polarization pattern.
Its rotation by
, m=0 polarization pattern.
Its rotation by ![]() is also a valid configuration (purple lines).
This represents a pure NW-SE (and by sign reversal NE-SW), or U-polarization
pattern. We return in §3.3 to consider the geometrical distinction
between the two patterns, the electric and magnetic modes.
is also a valid configuration (purple lines).
This represents a pure NW-SE (and by sign reversal NE-SW), or U-polarization
pattern. We return in §3.3 to consider the geometrical distinction
between the two patterns, the electric and magnetic modes.
Fig. 4: Polarization pattern for l=2, m=0 (note the azimuthal symmetry). The scattering of a scalar m=0 quadrupole perturbation generates the electric E (yellow, thick lines) pattern on the sphere. Its rotation by 45 degrees represents the orthogonal magnetic B (purple, thin lines) pattern.
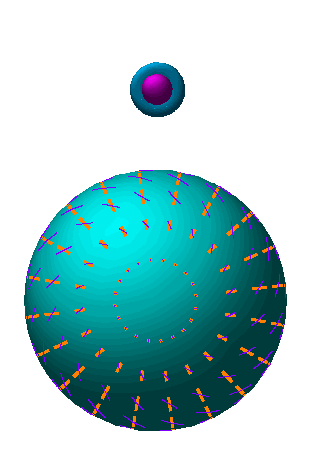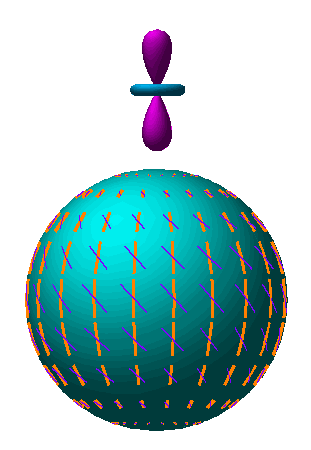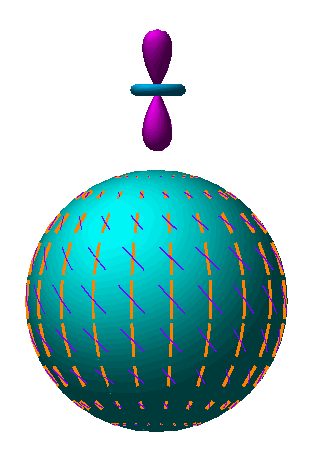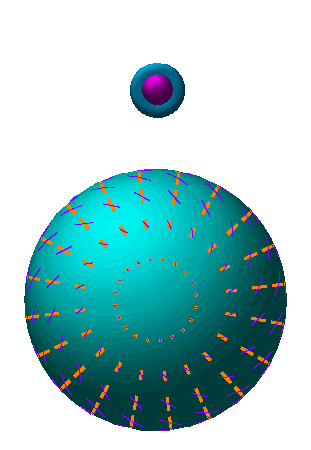
Animation: As the line of sight n changes, the lobes of the quadrupole rotate in and out of the tangent plane. The polarization follows the orientation of the colder (red) lobe in the tangent plane.
Next: Vector Perturbations