We have provided a new technique for the study of temperature and polarization anisotropy formation in the CMB which introduces a simple and systematic representation for their angular distributions. The main virtue of this approach is that the gravitational and scattering sources are directly related to observable properties in the CMB. One can then explore properties that are independent of the source, which tell us the broad framework, e.g. the classical cosmological parameters and the nature of fluctuations in the early universe, and identify properties that are dependent on the source, which can help pin down the model for structure formation. An example of the former is the fact that scalar fluctuations generate no magnetic parity polarization [3,4], vectors generate mainly magnetic parity polarization, and tensors generate comparable but somewhat smaller magnetic parity polarization. Large angle polarization of the three components are also constrained by model-independent geometric arguments in its slope and its correlation with the temperature anisotropy. If the scalar contributions can be isolated from the vectors, tensors and other foreground sources of polarization from these and other means, these constraints translate into a robust distinction between isocurvature and adiabatic models for structure formation.
In our representation, the temperature and polarization distributions are projections on the sky of four simple sources, the metric fluctuation (via the gravitational redshift), the intrinsic temperature at last scattering, the baryon velocity at last scattering (via the Doppler effect) and the temperature and polarization quadrupoles at last scattering (via the angular dependence of Compton scattering). As such, it better reveals the power of the CMB to probe the nature of these sources and extract information on the process of structure formation in the universe. As an example, we have explored how general properties of scaling stress seeds found in cosmological defect models manifest themselves in the temperature and polarization power spectra. The framework we have provided here should be useful for determining the robust signatures of specific models for structure formation as well as the reconstruction of the true model for structure formation from the data as it becomes available.
Acknowledgements: We would like to thank Uros Seljak and Matias Zaldarriaga for many useful discussions. W.H. was supported by the W.M. Keck Foundation.
TAB-2. Commonly used symbols. ![]() for the scalars, vectors, and
tensors. For the fluid variables
for the scalars, vectors, and
tensors. For the fluid variables ![]() for the photons,
for the photons,
![]() for the baryons and
for the baryons and ![]() for the photon-baryon fluid.
for the photon-baryon fluid.
![]() , E, B for the temperature-polarization power spectra.
, E, B for the temperature-polarization power spectra.
| Symbol | Definition | Eqn. |
| Scalar metric | (36)
|
|
| |
(55)
|
|
| Euler angles | (7)
|
|
| Radial B,E function | (16)
|
|
| Fluid density perturbation | (39)
|
|
| Conformal time | (35)
|
|
| Clebsch-Gordan coefficient | (59)
|
|
| Fluid, seed density | (39)
|
|
| Fluid, seed anisotropic stress | (39)
|
|
| Spherical coordinates in |
(10)
|
|
| Thomson optical depth | (49)
|
|
| B-pol. moments | (55)
|
|
| Collision term | (50)
|
|
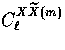 |
|
(56)
|
| E-pol. moments | (55)
|
|
| Gravitational redshift term | (54)
|
|
| Temperature basis | (10)
|
|
| Polarization basis | (11)
|
|
| H | Tensor metric | (38)
|
| (Pauli) matrix basis | (1)
|
|
| P(m) | Anisotropic scattering source | (62)
|
| Q(0) | Scalar basis | (26)
|
| Q(1)i | Vector basis | (28)
|
| Q(2)ij | Tensor basis | (32)
|
| R | |
(66)
|
| Temperature source | (61)
|
|
| V | Vector metric | (37)
|
| |
Spin-s harmonics | (2)
|
| Radial temp function | (15)
|
|
| Wavenumber | (10)
|
|
| kD(m) | Damping wavenumber | (98)
|
| Multipole | (2)
|
|
| Effective mass 1+R | (80)
|
|
| Propagation direction | (12)
|
|
| pf, ps | Fluid, seed pressure | (39)
|
| vf(m) | Fluid velocity | (39)
|
| vs(m) | Seed momentum density | (39)
|
| wf | |
(65)
|