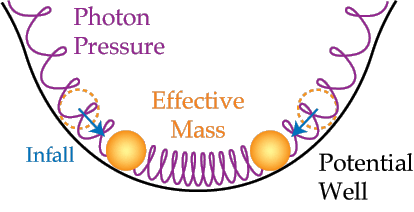
The most prominent and useful features in the anisotropy of the CMB come from acoustic oscillations of the photon-baryon fluid. Radiation pressure from the photons resists the gravitational compression of the fluid into potential wells and sets up acoustic oscillations in the fluid:
Figure:Radiation Pressure and Gravity
Springs represent photon pressure and balls represent the effective mass of the fluid.
The shorter the wavelength of the potential fluctuation the faster the fluid oscillates such that at last scattering the phase of the oscillation reached scales with the wavelength. Since regions of compression (maxima) represent hot regions and rarefaction (minima) cold regions, there will be a harmonic series of peaks in wavelength associated with the acoustic oscillations. It is the features of these peaks that provide us with an array of cosmological tests.
Figure:Acoustic Oscillations
Displayed here is the time evolution of a single wavelength of the potential fluctuation (Fourier amplitude time evolution on right).
Technical note: Since the photons must climb out of the potential wells at last scattering, the effective temperature, &Theta+&Psi, is reduced at long wavelengths to 1/3 &Psi. This effect is commonly known as the Sachs-Wolfe effect.