Realistic models involve time-dependent potentials giving rise to forced oscillations in the photon-baryon fluid. This allows one to cleanly separate two competing models for structure formation cleanly from the CMB: adiabatic and isocurvature models. Adiabatic fluctuation, of which inflation is the unique causal generator, begin with gravitational potential wells established in the very early universe. On the other hand isocurvature models, begin with no potential fluctuations. They are only generated as matter is moved around inside the causal horizon. Cosmological defects provide isocurvature conditions (see e.g. Crittenden & Turok 1995 for textures), but there are other more phenomenologically based models.
The behavior of the potential wells, in particular the feedback influence of density perturbations generated by the acoustic oscillations on the potential wells themselves, serve to distinguish the two general cases:
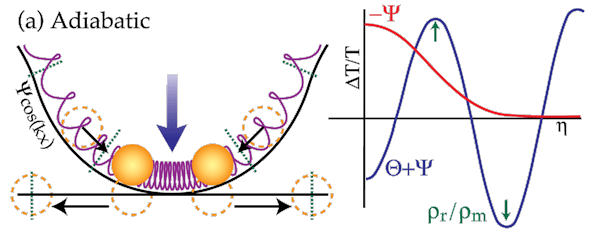
Figure: Adiabatic Case
As the fluid begins to compress, photon pressure resists the increase in the density perturbation, thereby allowing the gravitational potential to decay. Left in a highly compressed state, the fluid then oscillates as a cosine wave with enhanced amplitude.
Now let us consider the isocurvature case:
Figure: Isocurvature Case
Radiation fluctuations are here set up to eliminate the potential initially. Photon pressure resists the implied rarefaction of the fluid. The fluid then falls back into the well, lending its self-gravity to enhance the depth. At the compressional maxima, photon pressure again causes potential decay leaving the fluid in a highly compressed state. However, here it drives a sine oscillation.
Because the two general classes of perturbations drive different harmonics (cosine vs. sine), they can be cleanly distinguished by taking the ratios of the locations of the peaks (see Hu & White 1996a for concrete models):
Figure: Adiabatic vs. Isocurvature from Hu & White (1996b)
However, isocurvature models (e.g. cosmic strings) can also have strong effects after horizon crossing which can wash out these signals (see Magueijo et al. 1995 ). Likewise adiabatic models could be reionized and lose their peak structure.
These feedback effects increase with the radiation-matter density ratio allowing a measure of the matter-radiation equality epoch. Ignoring diffusion damping, we see that the peak heights in the adiabatic model rise by a factor of approximately 25 (20 in the presence of realistic neutrino content) through the equality scale:
Figure: Shape Parameter and Equality from Hu & White (1997)
leading to a probe analogous to the shape parameter of large scale structure but in anticorrelation with the latter effect. The ability to measure the equality epoch allows for a sensitive probe of the total matter content of the universe:
Animation: Matter Content Sensitivity. The matter-radiation ratio is raised while keeping all other parameters fixed (Omega0h2= 0.1-1)
PS Figure: From Hu & White (1996a)
With highly sensitive measurements there is even the possibility of measuring properties of the radiation such as the neutrino mass (see Ma & Bertschinger 1995 and Dodelson, et al. 1995).