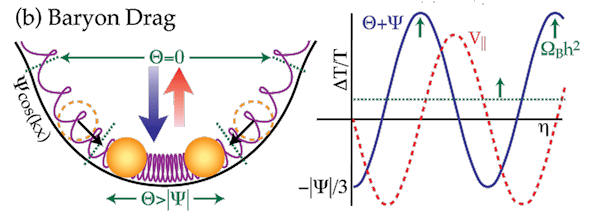
Baryons increase the effective mass of the fluid. This changes the balance between pressure and gravity in the fluid. Gravitational infall now leads to greater compression of the fluid in the potential well. Just like a mass on a spring, gravity shifts the zero point of the oscillator:
Figure: Baryon Drag
This increases the amplitude of the oscillation, since the initial conditions now represent a larger displacement from the zero point. More importantly it changes the absolute value (rms, dotted lines) of the maxima vs. minima of the effective temperature fluctuation. Compressions are enhanced over rarefactions of the fluid inside potential wells. Thus the relative heights of the peaks present one way of measuring the baryon content of the universe. In the scale-invariant adiabatic model, this is how the anisotropy depends on the baryon content:
Animation & 3Dplot: Change in peak heights as the baryon content is raised (h=0.5 -> Omegabh2 = 0.00125-0.125)
PS Figure: Baryon Sensitivity from Hu & White (1996a)
Baryons increase the amplitude of the oscillations as well as cause an alternation in the odd and even peak heights. Their effect on the damping tail is discussed further here.