Accurate theoretical anisotropy power spectra for popular models have long been available and codes to calculate them are now fast and public (e.g. Seljak & Zaldarriaga 1996). Here we will concentrate on the gross features of the spectrum which are likely to occur in most models.
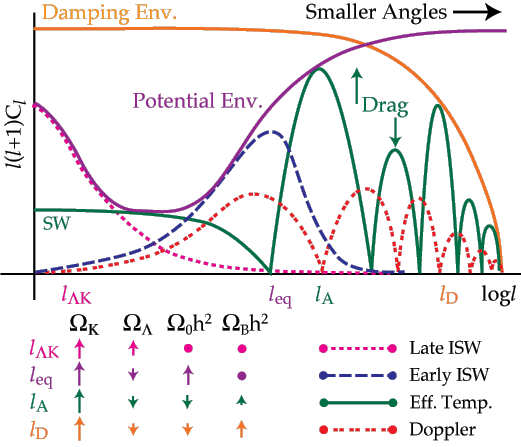
The physical scales associated with the acoustic (A), matter-radiation equality (eq), damping (D),and late ISW (KLambda) anisotropy formation mechanisms are imprinted on the anisotropy power spectrum.
Figure: Cosmological Parameter Dependence
A scale-invariant adiabatic example. Power spectrum of temperature anisotropies in multipole space (l is proportional to the inverse of the angle). Independent of these scalar effects, there may be tensor contributions below the acoustic scale in l .
The exact dependence of the anisotropies on these scales depends on the model for structure formation through the potential envelope that governs ISW and acoustic effects. Nevertheless, these four physical scales are generically imprinted on the CMB unless secondary anisotropies, e.g. from reionization dominate. Once measured, these four scales can be combined to extract four fundamental cosmological parameters in a robust fashion: the curvature, cosmological constant, matter-radiation ratio (Omega_0 h^2), and baryon-photon ratio (baryon content Omega_B h^2). Furthermore consistency checks can be made with some model assumptions. In adiabatic models, baryon drag provides another measure of the baryon content through the alternating peak heights and the shape of the large scale structure power spectrum checks the inferred matter-radiation ratio.