Early ISW Effect: The early ISW effect arises if the universe is not completely matter dominated at last scattering. In an adiabatic model, radiation pressure makes the potentials decay inside the sound horizon. Hence the potential fluctuation in a particular wavelength decays as the horizon grows past the wavelength. Wavelengths between the sound horizon at last scattering and at full matter domination can have strongly enhanced anisotropy contributions from this effect. These join smoothly onto driven acoustic contributions and form a potential envelope for the anisotropies.
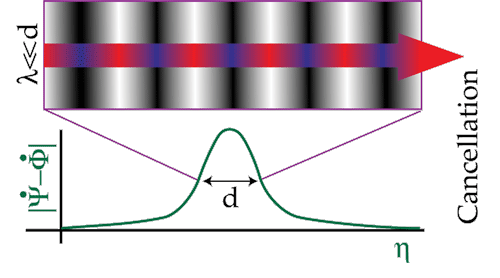
Late ISW Effect: In an open or lambda model, the universe enters a rapid expansion phase once matter no longer dominates the expansion. As density fluctuations are frozen in, the potential again decays leading to an ISW effect. Opposing effects from decaying overdensities and underdensities tend to cancel if the photons can travel across many wavelengths during the decay:
Figure: Late ISW Cancellation
as is the case for fluctuations under the horizon size at the end of matter domination. This scale is projected onto a large angle in the anisotropy spectrum both because of the intrinsically large size of the horizon at such late epochs and because the point of origin of the effect is much closer than the last scattering surface. This makes the same physical scale subtend a much larger angular scale :
Figure: Angular vs. Physical Scale from Hu & Sugiyama (1995b),
Contributions to the anisotropy in a Lambda model as a function of both angle (multipole l) and physical scale (wavenumber k). The projection takes secondary contributions such as ISW effects from the same physical scale to a larger angular scale than the primary Sachs-Wolfe (SW) effect. The ridgelike structure of the contributions comes from the projection of plane waves onto the sphere (Bessel function oscillations). The observable angular power spectrum comes from integrating in k the anisotropy contributions for each multipole (see Hu & White (1995), especially this figure).
For a fixed matter density, matter domination ends sooner in an open than a lambda universe. Thus the angular scale of the cancellation cut off in the spectrum is larger in a lambda universe.
Rees-Sciama Effect: Once fluctuations leave the linear regime, their subsequent evolution can also make the potentials vary with time. In hierarchical models, where the smallest scales go non-linear first, the effect peaks toward small scales. In most reasonable models, the non-linear scale is too small to significantly affect CMB observations above the arcminute regime (see Seljak 1996a, especially this figure). Although not likely to be observable by the next generation of experiments, the scale at which fluctuations become nonlinear is in principle also imprinted on the CMB.
Tensors: Gravitational waves introduce tensor fluctuations in the metric. As we have seen, distortions in the spatial metric can produce gravitational redshift effects on the photons. The difference here is that they leave behind a quadrupole signature. As with the other ISW effects only scales above the horizon at last scattering contribute. Hence the signature of tensor contributions is an enhanced quadrupole and a cut-off at the horizon at last scattering (see e.g. Hu et al. (1995), this figure). Inflation predicts a consistency relation between the gravity wave and density fluctuations which may provide a sensitive test of that paradigm (see e.g. Knox & Turner (1994))