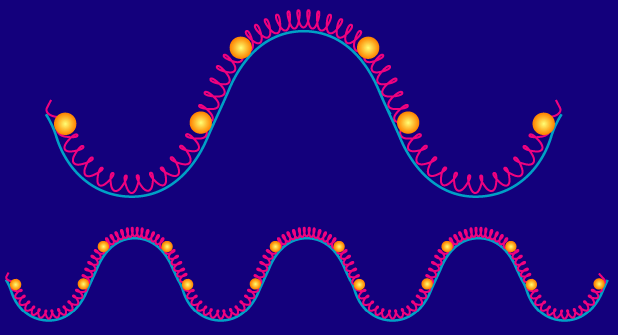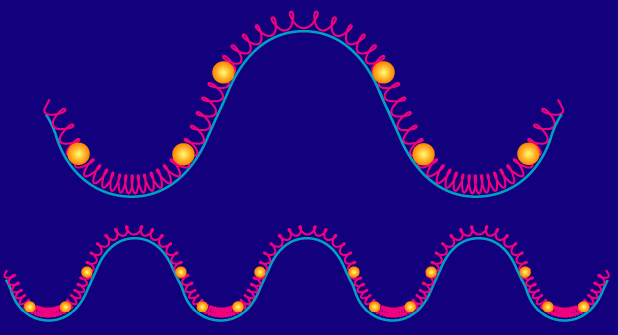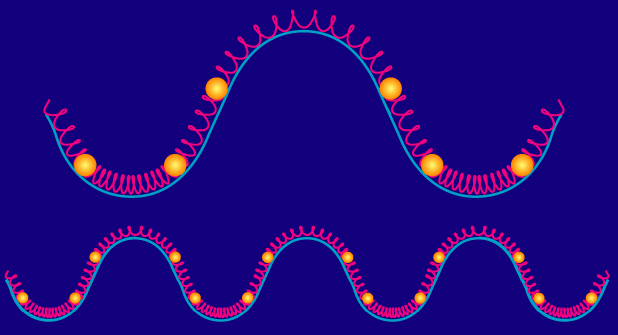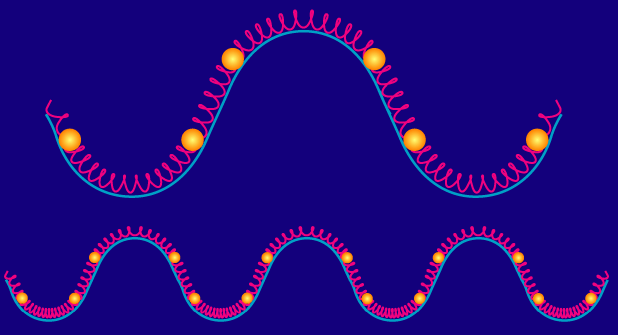
The final subtlety is that inflation lays down potential fluctuations on all scales. Mathematically we take the potential fluctuation in space and Fourier decompose it into plane waves of various wavelengths. Each of these wave-modes behave independently and so we can think of each individually.
There is however a special relationship between the temporal behavior of modes whose wavenumbers are related by integral multiples:

Because it takes half as long for the fluid to compress into a potential of half the length scale, the bottom mode in the figure oscillates exactly twice as fast as the top mode. Mathematically the frequency of the oscillation is equal to the wavenumber times the speed of sound: ω= kcs.