We know that the universe has been ionized at least until z = 5 from the null detection of the Gunn-Peterson effect. Hence after standard recombination at z = 1000 , the universe must have underwent reionization. However, the amount of rescattering of CMB photons is negligible unless the ionization persists through redshifts of several tens. This is unlikely in models without excessive small scale power and in such models, e.g. scale invariant adiabatic ones, degree scale anisotropy detections are already severely constraining the amount of reionization allowable. Still, it is useful to recall the basic physical effects associated with reionization.
Figure: Reionization Effects from Hu & White (1995)
Rescattering Damping: Rescattering damps fluctuations in the same manner as diffusion. Scattering eliminates anisotropies leaving them only in the unscattered fraction exp(-optical depth). Since outside the horizon, streaming has not yet converted temperature fluctuations to anisotropies, power is only lost below the horizon at the rescattering epoch.
Doppler Effect: Diffusion and rescattering prevents the appearance of large temperature fluctuations. However, the Doppler effect from scattering off electrons caught in the gravitational instability of the baryons can regenerate anisotropies. These contributions are suppressed in the same way as the late ISW effect:
Figure: Cancelled Doppler Effect from Hu (1995)
Photons that last scattered off opposite sides of the perturbation get Doppler shifted by equal and opposite amounts. Thus for wavelengths far below the thickness of the last scattering surface, Doppler contributions tend to cancel leaving a negligible net effect.
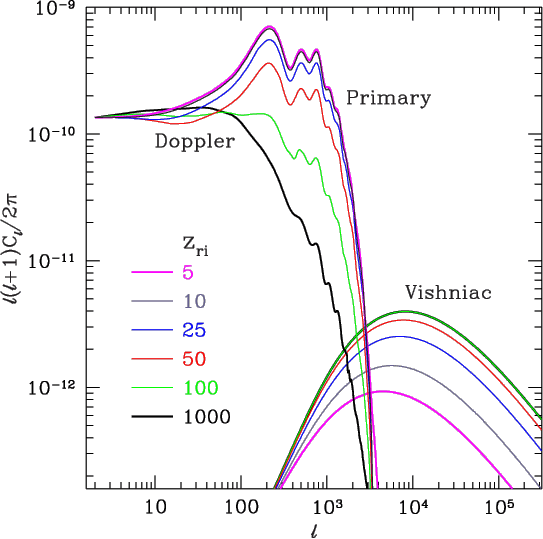
Non-linear Effects: At very small scales, higher order contributions are more efficient than the Doppler effect in regenerating anisotropies. These generally make use of combining the Doppler effect with variations in the optical depth. For example, the enhanced baryon density in an overdense region leads to preferential scattering in those regions. If the perturbations are also caught up in a bulk flow, then a Doppler shift arises that can escape cancellation (known as the Vishiac or Ostriker-Vishniac effect):
Figure: Vishniac Mechanism from Hu (1995)
Similarly, inhomogeneities in the ionization fraction, or contributions from clusters (kinematic Sunyaev-Zel'dovich effect) can give Doppler contributions. Clusters can also produce anisotropic spectral distortions due to the upscattering in frequency of photons by hot electrons (thermal Sunyaev-Zel'dovich effect).
Again, in models without high amplitude small-scale power, it is unlikely that any of these effects will dominate the total anisotropy in the observable regime.