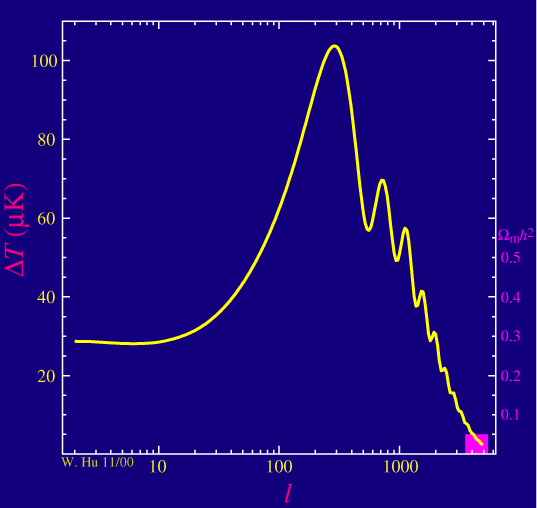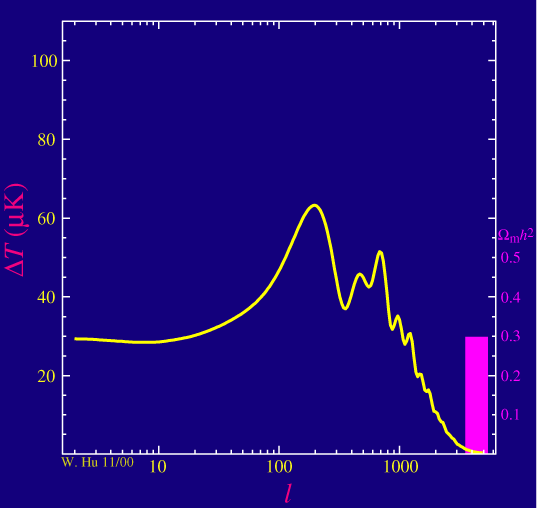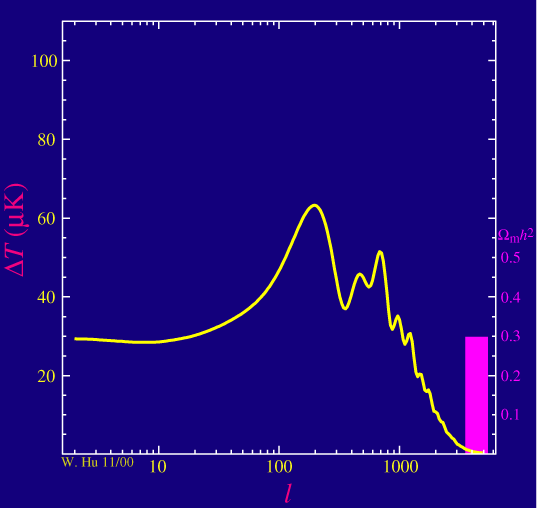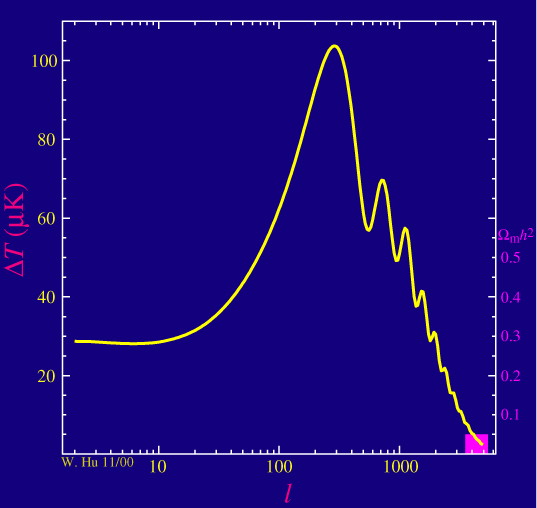
As advertised the acoustic peaks in the power spectrum are sensitive to the dark matter density in the universe. (Formally, the matter to radiation ratio but the radiation density is fixed in the standard model.)

As we raise the physical density of the dark matter, Wmh2, the driving effect goes away at a given peak such that its amplitude decreases. Although this effect changes the heights of all the peaks, it is only separable from the baryonic effects with at least three peaks. Note that decreasing the matter density also affects the baryon loading since the dark matter potential wells go away leaving nothing for the baryons to fall into. Having a third peak that is boosted to a height comparable to or exceeding the second peak is an indication that dark matter dominated the matter density in the plasma before recombination. Note that the self-gravity of the photons and baryons still plays a role in the first and second peaks so that the third peak is the cleanest test of this behavior.
Notice also that the location of the peaks, and that of the first peak in particular, changes as we change the dark matter density. The matter to radiation ratio also controls the age of the universe at recombination and hence how far sound can travel relative to how far light travels after recombination. This is the leading order ambiguity in the measurement of the spatial curvature of the universe. We see here that that ambiguity will be resolved when at least three peaks are precisely measured.