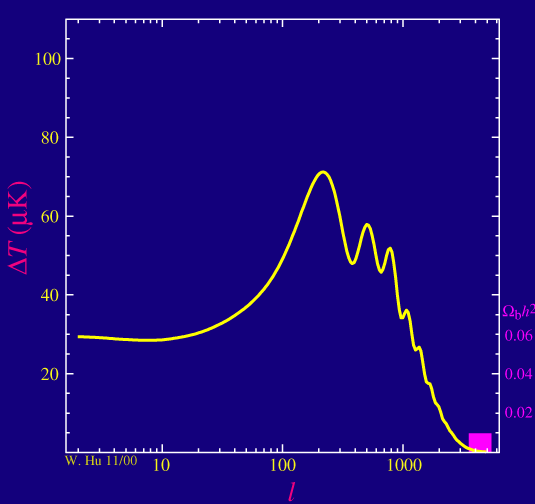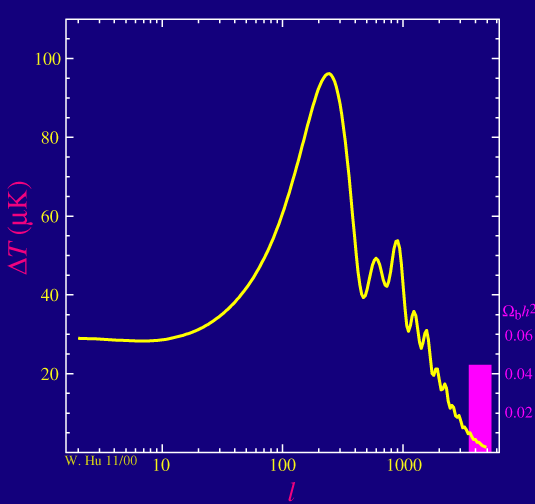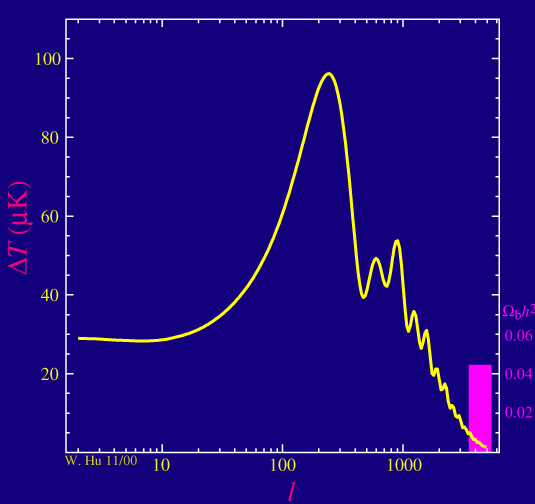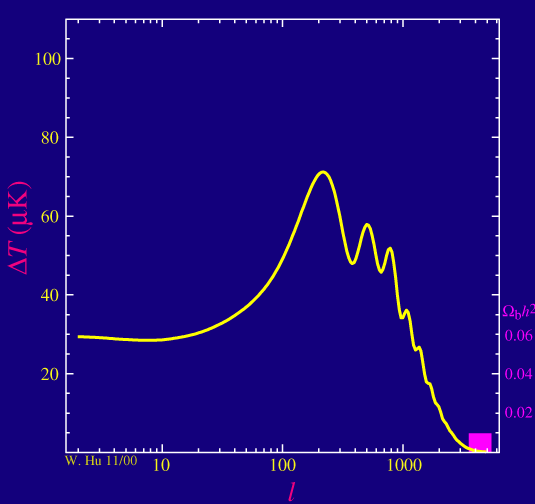
When we do the full calculation of the power spectrum, the basic physics of a mass on the spring appears as advertised. The odd numbered acoustic peaks in the power spectrum are enhanced in amplitude over the even numbered ones as we increase the baryon density of the universe.

[Note: Cosmologists label the baryon density in terms of its fraction of the critical density Wbtimes the Hubble constant squared (in units of 100 km/s/Mpc) to get something proportional to the physical density of the baryons.]
There are two other related effects due to the baryons: since adding mass to a spring slows the oscillation down, adding baryons to the plasma decrease the frequency of the oscillations pushing the position of the peaks to slightly higher multipoles l.
Baryons also affect the way the sound waves damp and hence how the power spectrum falls off at high multipole moment lor small angular scales as we will see later.
The many ways that baryons show up in the power spectrum imply that the power spectrum has many independent checks on the baryon density of the universe. The baryon density is a quantity that the CMB can measure to exquisite precision.