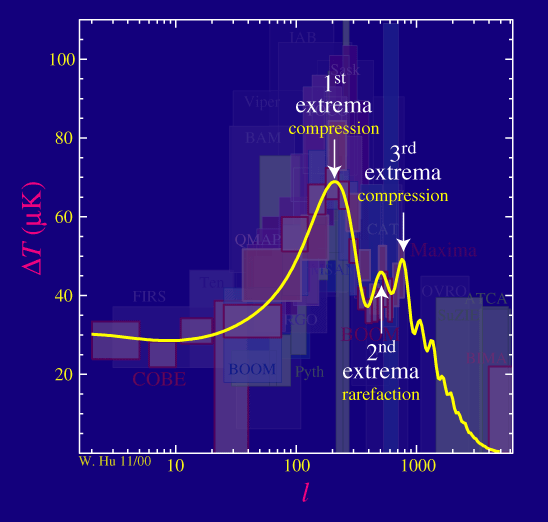
Okay, lets put this all together.
Modes caught at extrema of their oscillations become the peaks in the CMB power spectrum. They form a harmonic series based on the distance sound can travel by recombination, called the sound horizon. The first peak represents the mode that compressed once inside potential wells before recombination, the second the mode that compressed and then rarefied, the third the mode that compressed then rarefied then compressed, etc:

We see these spatial variations in the temperature as angular fluctuations on the sky since the CMB photons stream unimpeded to us from the time of recombination. The fundamental physical scale is then converted to a fundamental angle that is about a degree on the sky today. By analogy to spatial wavenumber k, we define an angular wavenumber, or multipole l as roughly the inverse of this angular scale (in radians). The fundamental angular wavenumber or multipole is l~200.