In the previous discussion, we've seen that the acoustic peaks will provide precise measurements of the angular diameter distance to recombination (mainly the curvature of the universe), the baryon density, and the dark matter density of the universe. In addition, they will measure the slope of the initial spectrum of gravitational potential fluctuations from inflation.
How well can a given experiment measure these cosmological parameters? Are their other cosmological parameters that the CMB peaks can measure?
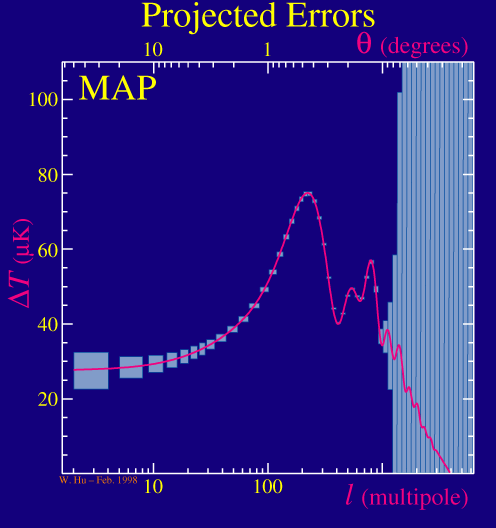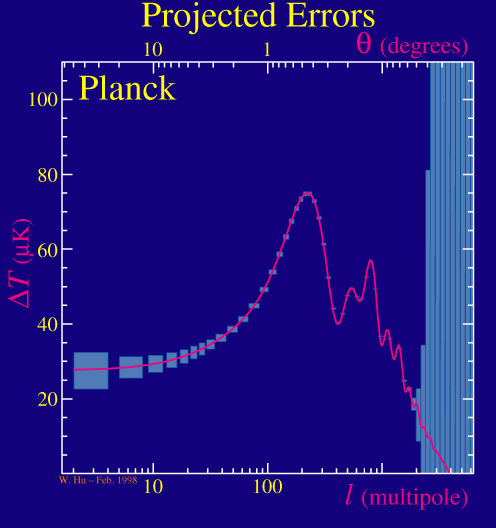
First let's see how well a given experiment can measure the power spectrum itself. There are two fundamental statistical limitations to the measurements. The first is the instrumental noise and the angular resolution of the experiment. These limit the amount of information on the high multipoles in the spectrum. For example, take the MAP satellite that is due to launch in the middle of 2001 and compare it to the Planck satellite that is due for a 2007 launch:

The higher resolution and lower noise of the Planck satellite allows it to measure further out into the series of acoustic peaks and so gather more information from them. Notice however that both experiments have the same errors at low multipoles or large angular scales.
At large angular scales both experiments are limited by the fact that we only have one sky to measure and so cannot pin down the cosmic average to infinite precision no matter how good the experiment is. Mathematically, there are only 2l+1 samples of the power at each multipole. In fact, the current generation of experiments that measure the peaks are even more severely limited in that they measure only a small fraction of the sky and so have an even smaller number of samples at each multipole (2l+1)fsky, where fsky is the fraction of the sky sampled.
This effect is called sample variance for a small patch of sky and cosmic variance for the full sky.