Now we can understand where the peaks come from.
Sound waves stop oscillating at recombination when the baryons release the photons. Modes that reach extrema of their oscillation (maximal compression or rarefaction in potential wells) by recombination will carry enhanced temperature fluctuations.
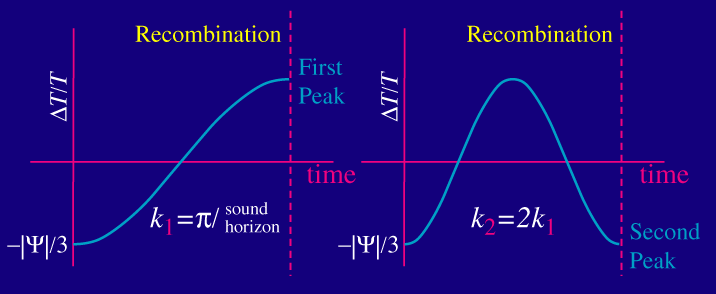
Let's plot the temperature fluctuation at say the bottom of a potential well of a mode of a given wavenumber (inverse wavelength) k1. It will oscillate in time as the fluid compresses and rarefies. There is a special mode for which the fluid just has enough time to compress once before recombination:

Mathematically the wavenumber (2π/wavelength) of this mode (k1) is equal to π divided by the distance sound can travel by recombination. This distance is called the sound horizon at recombination.
Because the mode with twice the wavenumber (half the wavelength) oscillates twice as fast, we know that there is a mode k2=2k1 which just has time to compress and then rarefy before recombination. Likewise there is a mode k3=3k1 which just has time to compress and then rarefy and then compress again. These modes represent the first, second and third peaks respectively. They are harmonics of the fundamental scale ? the distance sound can travel before recombination.
A helpful way to remember the principle behind this harmonic relation is to recall what happens to sound in a cavity of a musical instrument. There are frequency harmonics of the fundamental tone. In this case, the cavity is actually the amount of time before recombination and thus there exists a fundamental frequency as well. Because sound travels at a fixed speed we can also associate a fundamental scale to this frequency. That scale is exactly the distance sound can travel in the amount of time before recombination. Don't take this analogy too far: the waves are still incoherent in space so the waves would "sound" like noise not music.