If we can calibrate the distance CMB photons random walk during recombination, we have another standard ruler for the angular diameter distance test of the spatial curvature of the universe. Remember that we measure its angular scale in the power spectrum itself.
Alternatively, if we know the curvature of the universe we can infer the physical distance the photons travel. In the standard model, the physical distance depends only on the baryon density and the dark matter density (matter-radiation ratio). Since all three (curvature, baryons density and matter radiation) are measured by the positions and heights of the peaks themselves, the damping tail provides a beautiful consistency test for the standard model.
Let's see how that works.
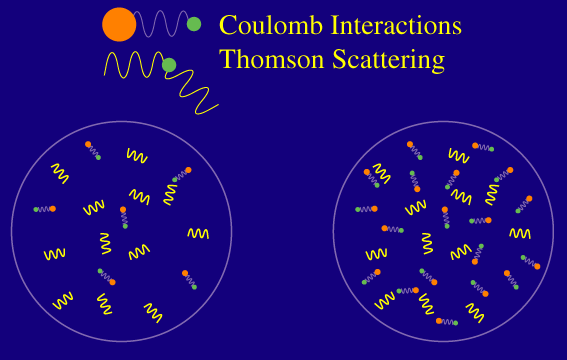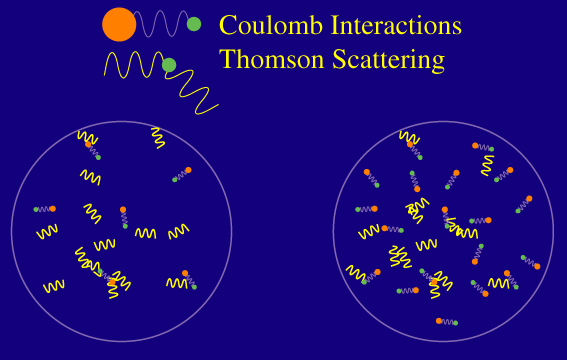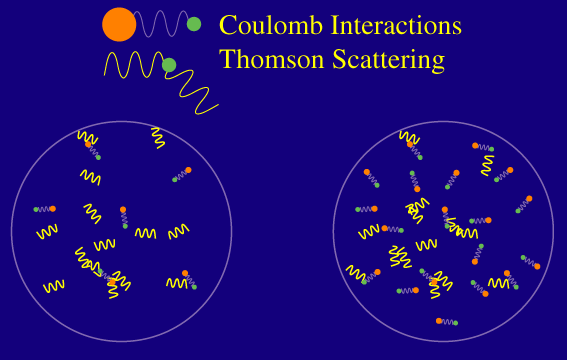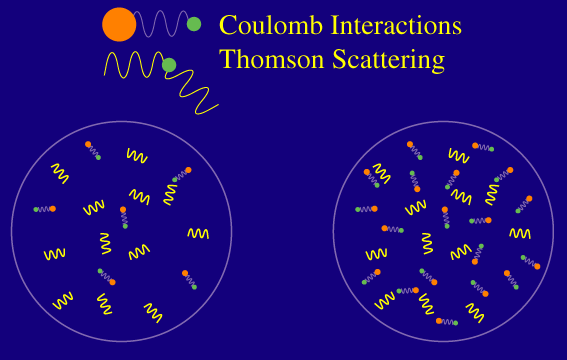
Microphysically, the distance photons can travel is related to a random walk process. Remember that the photons have a certain mean free path in the baryons defined as the average distance the photon travels before Thomson scattering off a free electron:

Raising the number of baryons, decreases the mean free path and hence shortens the distance photons can travel at recombination. Finally the full distance also depends on the amount of time the photons have to random walk and hence the age of the universe at recombination. Remember that the age is determined by the dark matter density. Mathematically, the length is roughly the geometric mean of the mean free path and the distance light can travel without obstruction (the horizon scale).