Ok so if what we are dealing with is actually noise in the technical sense, what do we do with it?
When dealing with noise, what we want to do is determine its spectral properties: is the noise white, red or blue? Does it have any features?
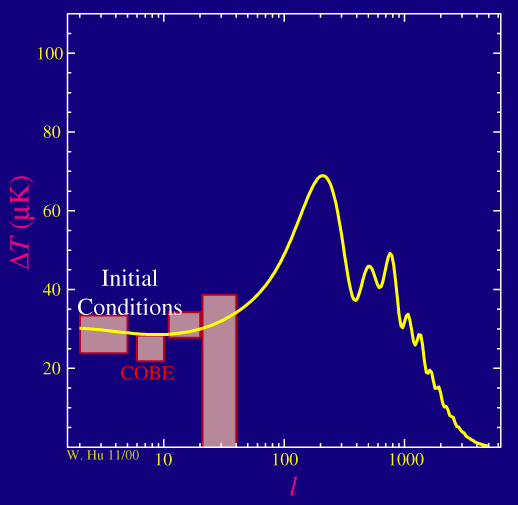
In this case when we speak of the spectrum of the noise, we are talking about the angular coherence of the temperature fluctuations rather than the temporal coherence of audible noise. Instead of temporal frequency, we speak of angular frequency called the multipole moment l. The reciprocal of lcorresponds to the angular scale which we will call the angular wavelength of the fluctuation. For example l=10 corresponds to roughly 10 degrees on the sky, l=100 corresponds to roughly 1 degree on the sky. Mathematically, the multipole moments arise from a spherical harmonic decomposition of the fluctuations in angle.
With its resolution of 7 degrees on the sky, the COBE satellite could only see the largest angle fluctuations:

The units on the y-axis are in micro (millionth of a) Kelvin. Since the temperature of the CMB is measured to be 2.73K, this makes the fluctuations 1 part in 100,000 as advertised. Mathematically, the power spectrum is actually equal to the square of this quantity times 2π/[l(l+1)], where the l's are there to account for the fact that the sky is two dimensional.
The first thing to note is that the COBE power spectrum (red boxes, 1 sigma errors and bandwidth of window) is far from white (or proportional to l in the above plot). There are correlations in the temperature on the largest angular scales. These scales are so large that there has not been enough time for the universe to evolve and so we are seeing mainly the initial fluctuations, the so-called initial conditions of the universe.
The second thing to note is that, as depicted in the yellow theoretical prediction, we expect there to be interesting things going on at l>100 or on angular scales below a degree. These structures are called the acoustic peaks.